Why Hexagons?

Source: Washington Post →

This visualization has a simple job: make TikTok’s algorithm visible.

To do that, the Washington Post attempts to analyze 121,000 videos from 1,100 users under a strict constraint: the model only sees viewing behavior.

Their article says that the algorithm doesn’t know what a video is about. It only knows who watched what. Any structure in the map is learned, not labeled.

But why hexagons?

Circles, Squares, and Hexagons

With a few hundred videos, you could plot individual points. With 121,000, that's going to get messy fast.

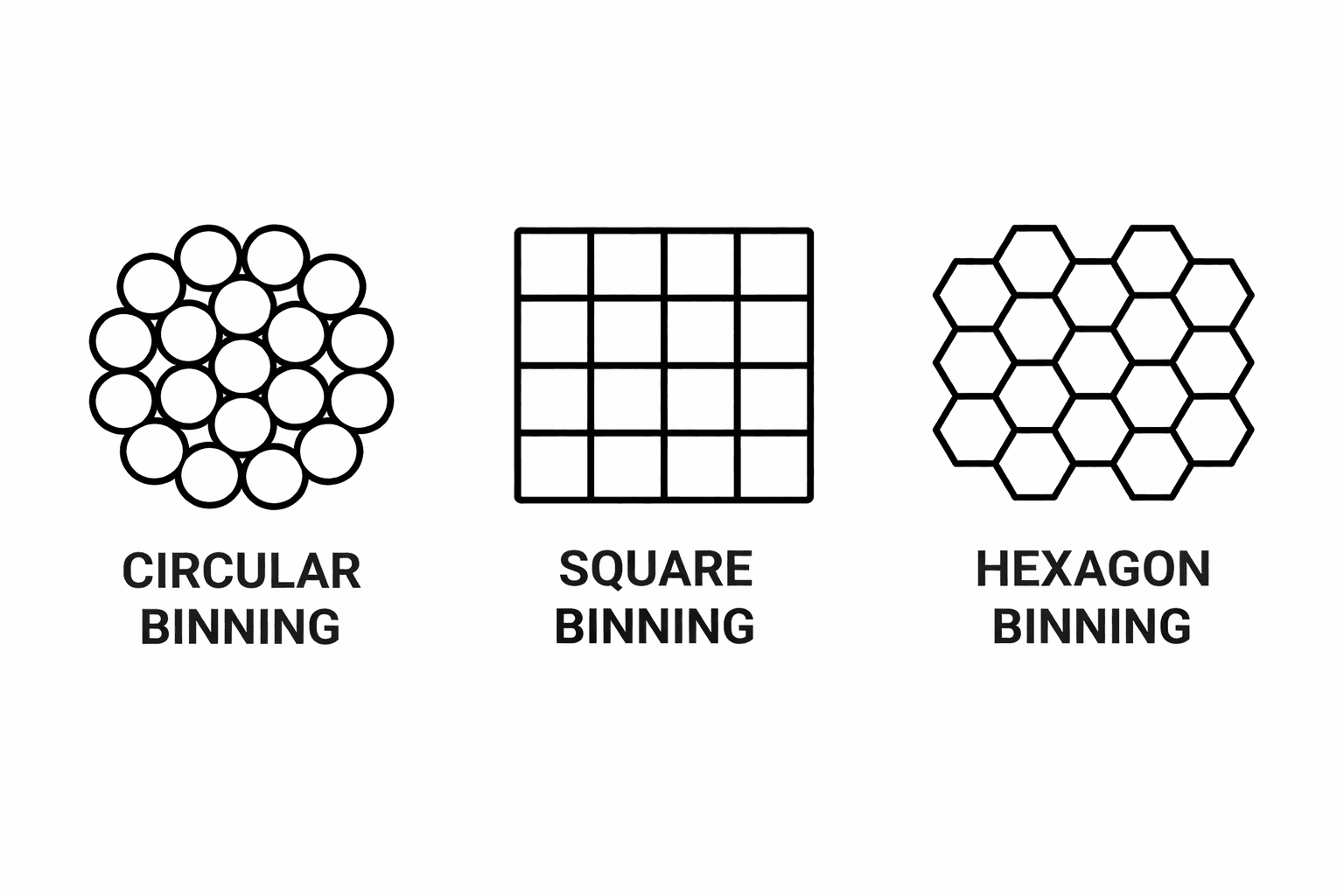
Binning allows the visualization to emphasize patterns between topic regions and how they relate spatially without the excessive clutter. But the choice of bin shape matters.

Circles are great as marks, but they don’t tessellate (tile the plane with no gaps or overlaps), so as “bins” the gaps they leave are visual clutter...

Squares do better. They tile cleanly, but after a while the grid visually starts to dominate with its strong horizontal/vertical edges.

And that lands us on Hexagons. They tile without gaps and their grid pattern is less visually harsh, so the regions feel more continuous. You could technically stop there, but we can get nerdier...

If you think of each bin as the “territory” around a representative point, the choice of bin shape is really a choice of lattice: where the bin centers live, and how neighborhoods connect.

A square grid is the Voronoi tessellation of a square lattice. That lattice has a strong axis structure: each site has 4 nearest neighbors, and the next 4 sit farther away on the diagonals (at √2 times the distance). This uneven neighbor geometry can make density patterns look slightly direction-biased along the axes.

A hex grid corresponds to the Voronoi tessellation of the triangular lattice (often described as “hexagonal packing” of points): each site has 6 nearest neighbors, all at the same distance. That more uniform local neighborhood is why hex-binned fields often read as more directionally “neutral.”

If you're interested in more details, Hexagon Binning: an Overview — Nicholas Lewin-Koh (Nov 13, 2024) dives into the math behind hexagonal binning.